dfs回溯
如何将1-9个数字排序?
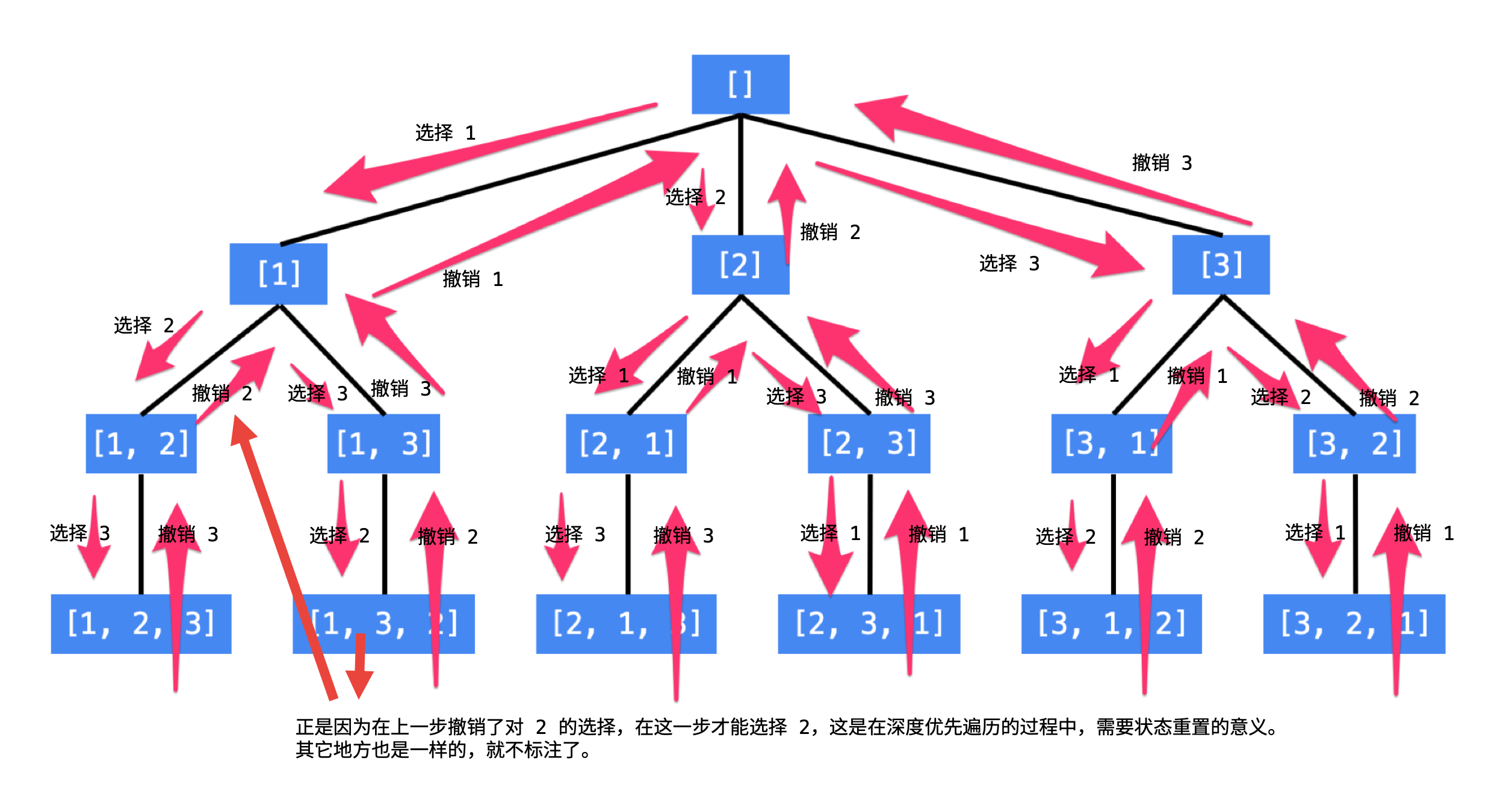
我们拿123来举例,
可以设置一个函数,通过递归调用的方式完成排序功能
将数组divide两半,排序过的和没排序过的。
第一子树取1 没排序的是2 3 接下来调用自身对2 3进行排序,
第二子树取2 没排序的是1 3 接下来调用自身对1 3进行排序,
第二子树取3 没排序的是2 3 接下来调用自身对2 3进行排序,
那么会有一个问题,取了2以后,我怎么知道没取的是2?可以将2移到已取的序列中,即移到本次递归的已排序序列的最后一个。我们用first来区隔已取和未取。
递归退出的条件是所有的数都在已排序的序列中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
output=[1,2,3,4,5,6,7,8,9];
dfs(1,9,output)
function dfs(first,n,output)
if(output(5)==1||output(1)>4||output(4)==1||output(9)==1)
%%分析容易得知,第二个乘数不可能为1,并且第一个乘数的千位不可能大于等于5
%%需要做一些预处理工作才能达到剪枝的目的。预处理工作虽然也消耗时间,但能够剪枝节约的时间更多;
return
end
%%从这里开始都是剪枝
firstnum=output(1)*1000+output(2)*100+output(3)*10+output(4);
z=firstnum*output(5);
if z > 9876
return;
else
a6=fix(z/1000);
a7=fix((z-a6*1000)/100);
a8=fix((z-a6*1000-a7*100)/10);
a9=fix(z-a6*1000-a7*100-a8*10);
if a6==a7||a6==a8||a6==a9||a7==a8||a7==a9||a8==a9
return
end
end
%%以上是剪枝
if(first+1==n)
isAns(output)
return
end
for i=first:n
temp=output(i);
output(i)=output(first);
output(first)=temp;
%用来交换output数组中索引first和i元素,移到本次递归的已排序序列的最后一个
dfs(first+1,9,output);
temp=output(i);
output(i)=output(first);
output(first)=temp;
%用来交换output数组中索引first和i元素,这一步为回溯的关键!
end
end
function isAns(output)
%用来判断是否找到结果
%即output的前4位乘第五位是否等于后4位
first=output(1)*1000+output(2)*100+output(3)*10+output(4);
last=output(6)*1000+output(7)*100+output(8)*10+output(9);
if first*output(5)==last
fprintf('%d * %d = %d\n',first,output(5),last)
end
end
|
一些优化,回溯,用于对空间进行优化
搜索问题的状态空间一般很大,如果每一个状态都去创建新的变量,时间复杂度是 O(N)O(N)。在候选数比较多的时候,在非叶子结点上创建新的状态变量的性能消耗就很严重。
