48. 旋转图像

48. 旋转图像

难度中等933收藏分享切换为英文接收动态反馈

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在** 原地** 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：
1
2
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]
示例 2：
1
2
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
示例 3：
1
2
输入：matrix = [[1]]
输出：[[1]]
示例 4：
1
2
输入：matrix = [[1,2],[3,4]]
输出：[[3,1],[4,2]]
提示：

matrix.length == n

matrix[i].length == n

1 <= n <= 20

-1000 <= matrix[i][j] <= 1000

通过次数192,922

提交次数263,618

一个很久就看到的题目，一直没写，不过上手发现思路不难。

观察旋转过程中坐标的变化,以3*3矩阵来举例：

(1,1)-> (1,3)

(1,2)->(2,3)

(1,3)->(3,3)

(2,1)->(1,2)

(2,2)->(2,2)

(2,3)->(3,2)

多写几个就可以发现规律了：(i,j)->(j,n+1-i)，这就意味着，将所有(i,j)位置上的值移到(j,n+1-i)位置上就行了，为了方便，可以另起一个矩阵，填入新值，就完成了。

注意下标是从0开始的，坐标转化应该是(i,j)->(j,n-1-i)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


public static void rotate(int[][] matrix) {
        int n_temp=matrix.length;
        int bb[][]=new int[n_temp][n_temp];
            // System.out.println(matrix.length);
        for( int i=0;i<matrix.length;i++){
            for(int j=0;j<n_temp;j++){

                bb[i][j]=matrix[i][j];
            }}

        for( int i=0;i<matrix.length;i++){
            for(int j=0;j<n_temp;j++){
                matrix[j][n_temp-1-i]=bb[i][j];
            }
        }

这就是一个最简单的旋转移动的思路了。可以拿一个图像试验一下，这里使用matlab

原始图片是这样，

使用matlab获得rgb值，进行旋转变换：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


tu = imread('image2022.png');

tu1=tu(:,:,1);
s=size(tu1)
tu2=zeros(s(2),s(1));

for i=1:s(1)
    for j=1:s(2)
    tu2(j,s(1)+1-i)=tu1(i,j);
    end
end
image(tu2)

得到的结果：

注意matlab中数组下标是从1开始的。

回到题目中来，题目要求请不要 使用另一个矩阵来旋转图像，怎么办？

观察(i,j)->(j,n+1-i)，能不能看成两步(i,j)->(n+1-i,j)，(n+1-i,j)->(j,n+1-i)

第一步是左右颠倒，(1,3)移到了(3,3);(3,3)移到了(1,3)，这样就可以交换了。

第二步是对称交换，根据对角线对称。

这样不需要使用另外一个矩阵进行保存数据了。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        // 水平翻转
        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < n; ++j) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - i - 1][j];
                matrix[n - i - 1][j] = temp;
            }
        }
        // 主对角线翻转
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
    }
}
//官方题解

第三种方法：

一次性移动4格，详见官方题解。（公式的复制出现问题了，不然我就粘贴在这里了）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


 public void rotate(int[][] matrix) {
        int n = matrix.length;
        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < (n + 1) / 2; ++j) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = temp;
            }
        }
    }

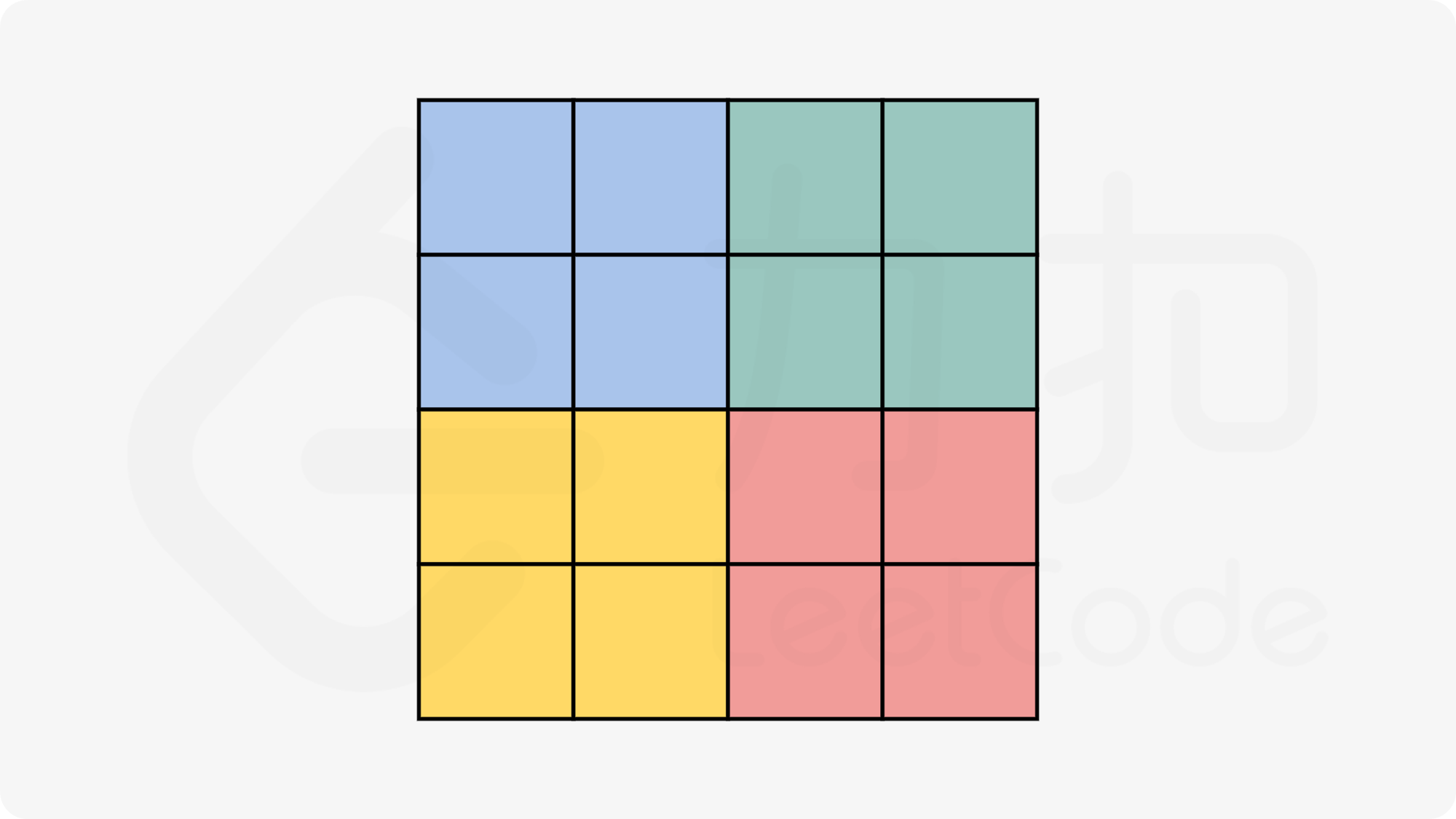
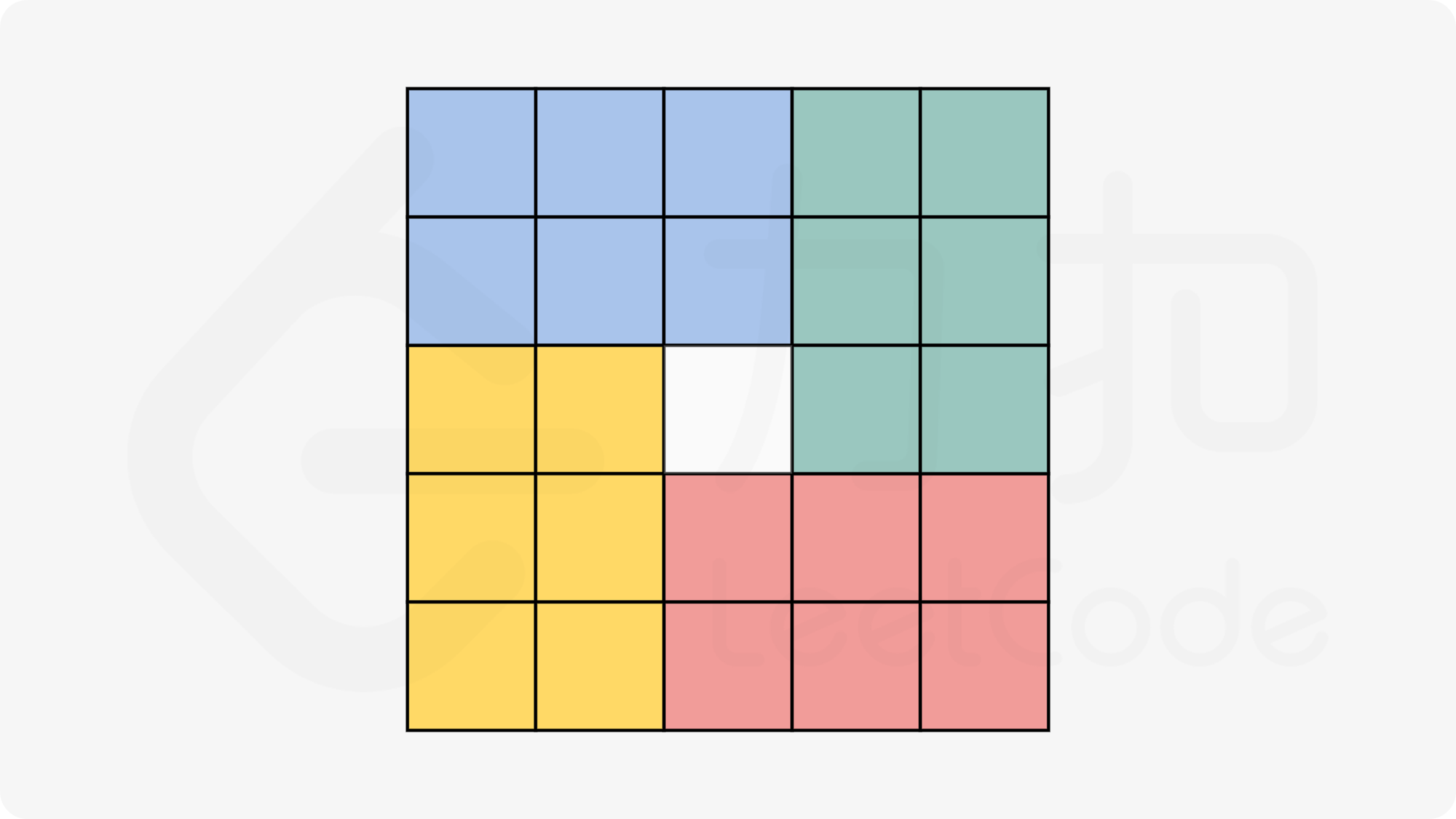
作者：LeetCode-Solution 链接：https://leetcode-cn.com/problems/rotate-image/solution/xuan-zhuan-tu-xiang-by-leetcode-solution-vu3m/ 来源：力扣（LeetCode）著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

8086

48.旋转图像

48. 旋转图像

48. 旋转图像